
| Солнечно-земная проект "СиЗиФ"
|
 |
Е.E. АнтоноваКонвекция и структура токов
| ч.1 |
Природа электрических полей и токов, регистрируемых в магнитосфере и ионосфере Земли, на протяжении многих лет продолжает волновать умы ученых-космофизиков. Данная проблема постоянно привлекала внимание проф. Б.А.Тверского (см. Тверской [1969, Tverskoy [1972], Тверской и Ташкинова 1972-75], Тверской [1982a,b], Аккуратов и др. [1972]). Работы, выполненные Б.А.Тверским в конце 60-х годов содержали ряд идей, оказавших большое влияние на ход последующих исследований, и были оформлены в качестве открытия “Явления электрического магнитосферно-ионосферного взаимодействия при крупномасштабном возмущении магнитосферы” (№ госрегистрации 369). В литературе в связи с проблемой магнитного пересоединения и природы электрического поля в магнитосфере Земли не утихают дискуссии по поводу основных использующихся соотношений. Поэтому имеет смысл обсудить природу токов в бесстолкновительной плазме с целью выбора описания плазмы наиболее адекватным для случая магнитосферы Земли образом. где c – скорость света. Скорости дрейфа в поле неэлектрической природы и неоднородном магнитном поле определяются соотношениями: где где При изотропном распределении частиц по питч-углам Дрейфовое приближение дает возможность описывать плазменную систему только в случае, когда кулоновскими столкновениями можно пренебречь (т.е. когда характерное время процесса где Вариации потоков электронов в овале (существование мультиплетных структур типа перевернутого V и авроральных дуг при этом, обусловлены вариациями продольного падения потенциала. Исследования, проведенные при пересечениях аврорального овала на спутниках (см. Wing and Newell [1998]), подтвердили выводы работ Антоновой и др. [1991, 1998] о постоянстве электронной и ионной температур частиц плазменного слоя. Так как ларморовский радиус электронов плазменного слоя намного меньше характерной неоднородности магнитного поля, наблюдаемая незамагниченность электронов может быть обусловлена взаимодействием с неоднородными электрическими полями или волнами. При этом в случае движения в неоднородных электрических полях эффективная стохастизация возникает, когда характерный масштаб неоднородности поля сравним с ларморовским радиусом частицы. Процесс стохастизации частиц при движении в неоднородном электрическом поле исследовался в работе Антоновой и др. [1998]. Несохранение магнитного момента во многих областях магнитосферы Земли приводит к необходимости замены дрейфового приближения на ряд более сложных. Часто при этом предполагается, что может быть использована классическая магнитная гидродинамика справедливая, когда характерное время процесса Одножидкостное магнитогидродинамическое (МГД) приближение для
где r
- плотность плазмы, V – скорость движения; уравнение движения (закон сохранения импульса):
где q – плотность потока тепла, Оно также предполагает соблюдение закона Ома в форме где согласно которому связь поперечного тока с градиентом давления совпадает с соотношением (5), полученным для случая бесстолкновительной плазмы описываемой дрейфовым приближением. Такое совпадение дает основание предполагать, что соотношение (11) будет справедливым и в случае бесстолкновительной плазмы не описываемой дрейфовым приближением, хотя данное утверждение и нельзя считать доказанным. В условиях магнитостатического равновесия, когда где
Основные выводы, содержащиеся в данных работах и использованный математический аппарат. обсуждаются в обзорах Антонова и Тверской [1996], Тверской и Антонова [1996]. За последнее время был получен ряд новых экспериментальных и теоретических результатов, проливающих свет на природу и основные свойства внутримагнитосферной конвекции. В настоящей работе будет рассмотрена эволюция основных представлений о природе внутримагнитосферной конвекции, и обсуждены пути дальнейшего развития теоретических и экспериментальных исследований.
Градиенты давления и электрические поля
в бесстолкновительной плазме
В однородных электрическом E и магнитном B полях электроны и ионы дрейфуют с одной и той же скоростью, не зависящей от массы частицы и знака заряда и равной
![]()
![]() ,
,![]() (1)
(1) 
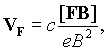
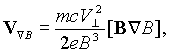
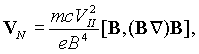 (2)
(2) ![]() перпендикулярная к магнитному полю и параллельная компоненты скорости. Таким образом, в бесстолкновительной плазме в первом приближении (без учета поляризационного дрейфа, являющегося дрейфом в сильно неоднородном или переменном во времени электрическом поле) электрическое поле не создает тока, а силы неэлектрической природы (например, гравитационная) и неоднородность магнитного поля могут приводить к возникновению токов. Ларморовское вращение частицы также является током с магнитным моментом m
=
перпендикулярная к магнитному полю и параллельная компоненты скорости. Таким образом, в бесстолкновительной плазме в первом приближении (без учета поляризационного дрейфа, являющегося дрейфом в сильно неоднородном или переменном во времени электрическом поле) электрическое поле не создает тока, а силы неэлектрической природы (например, гравитационная) и неоднородность магнитного поля могут приводить к возникновению токов. Ларморовское вращение частицы также является током с магнитным моментом m
=![]() , поэтому интегральный ток в неоднородном магнитном поле состоящий из дрейфового и диамагнитного тока, равен
, поэтому интегральный ток в неоднородном магнитном поле состоящий из дрейфового и диамагнитного тока, равен![]()
![]()
![]() (3)
(3) ![]() - дрейфовый ток,
- дрейфовый ток, ![]() - намагниченность плазмы на единицу объема,
- намагниченность плазмы на единицу объема, ![]() - заряд, масса и концентрация частиц сорта a
,
- заряд, масса и концентрация частиц сорта a
,![]() - усредненная скорость дрейфа,
- усредненная скорость дрейфа, ![]() - поперечная скорость частицы. Если
- поперечная скорость частицы. Если ![]() - параллельная и перпендикулярная компоненты тензора давления и
- параллельная и перпендикулярная компоненты тензора давления и ![]() , то ток в плазме равен
, то ток в плазме равен![]()
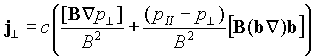 ,
, ![]() (4)
(4)
![]() и ток в плазме определяется соотношением
и ток в плазме определяется соотношением 
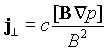
 (5)
(5) ![]() много больше характерного времени электрон-ионных столкновений
много больше характерного времени электрон-ионных столкновений ![]() и характерные масштабы неоднородности электрического и магнитного полей много больше ларморовского радиуса частиц. Характерное время кулоновских столкновений в магнитосферной плазме значительно больше характерных времен внутримагнитосферных процессов. Столкновения с нейтралами также крайне редки и учитываются только при анализе плазменных процессов в ионосфере. Поэтому первое условие применимости дрейфового приближения выполняется с большим запасом. К сожалению, второе условие в большинстве случаев не выполняется. Справедливость адиабатического приближения (описания движения частиц, при котором сохраняются адиабатические инварианты) удается обосновать для частиц радиационных поясов не очень больших энергий (см. Kuznetsov [1984]) и частиц кольцевого тока. Эффективность использования адиабатического приближения для описания движения частиц внутренней магнитосферы была продемонстрирована Б.А.Тверским(см. Б.А.Тверской [1968])при создании теории формирования радиационных поясов за счет магнитной диффузии (переноса частиц поперек дрейфовых оболочек электромагнитными полями внезапных импульсов). В плазменном слое магнитосферы Земли ларморовский радиус теплового иона сравним с радиусом кривизны магнитной силовой линии, что вызывает несохранение магнитных моментов ионов (см. Buchner and Zelenyi [1989], Chen and Palmadesso [1986]). В работах Антоновой и др. [1993], Antonova et al. [1996c] было показано, что не только ионы, но и электроны плазменного слоя незамагничены. Основным экспериментальным аргументом в пользу незамагниченного движения электронов плазменного слоя является отсутствие зависимости электронной температуры от широты (что возможно только в случае интенсивного перемешивания частиц плазменного слоя). Для структур типа перевернутого V, имеющих характерную протяженность по меридиану 50-200 км на ионосферных высотах, отсутствие зависимости электронной температуры от широты было установлено еще при экспериментальной проверке связи потока высыпающихся электронов
и характерные масштабы неоднородности электрического и магнитного полей много больше ларморовского радиуса частиц. Характерное время кулоновских столкновений в магнитосферной плазме значительно больше характерных времен внутримагнитосферных процессов. Столкновения с нейтралами также крайне редки и учитываются только при анализе плазменных процессов в ионосфере. Поэтому первое условие применимости дрейфового приближения выполняется с большим запасом. К сожалению, второе условие в большинстве случаев не выполняется. Справедливость адиабатического приближения (описания движения частиц, при котором сохраняются адиабатические инварианты) удается обосновать для частиц радиационных поясов не очень больших энергий (см. Kuznetsov [1984]) и частиц кольцевого тока. Эффективность использования адиабатического приближения для описания движения частиц внутренней магнитосферы была продемонстрирована Б.А.Тверским(см. Б.А.Тверской [1968])при создании теории формирования радиационных поясов за счет магнитной диффузии (переноса частиц поперек дрейфовых оболочек электромагнитными полями внезапных импульсов). В плазменном слое магнитосферы Земли ларморовский радиус теплового иона сравним с радиусом кривизны магнитной силовой линии, что вызывает несохранение магнитных моментов ионов (см. Buchner and Zelenyi [1989], Chen and Palmadesso [1986]). В работах Антоновой и др. [1993], Antonova et al. [1996c] было показано, что не только ионы, но и электроны плазменного слоя незамагничены. Основным экспериментальным аргументом в пользу незамагниченного движения электронов плазменного слоя является отсутствие зависимости электронной температуры от широты (что возможно только в случае интенсивного перемешивания частиц плазменного слоя). Для структур типа перевернутого V, имеющих характерную протяженность по меридиану 50-200 км на ионосферных высотах, отсутствие зависимости электронной температуры от широты было установлено еще при экспериментальной проверке связи потока высыпающихся электронов ![]() от продольной разности потенциалов
от продольной разности потенциалов ![]() , полученной в работах Knight [1973], Антоновой и Тверского [1975] и имеющей вид для случая достаточно удаленного от ионосферы падения потенциала,
, полученной в работах Knight [1973], Антоновой и Тверского [1975] и имеющей вид для случая достаточно удаленного от ионосферы падения потенциала,
![]() ,
,  (6)
(6)![]() ,
, ![]() - масса электрона,
- масса электрона, ![]() ,
, ![]() - концентрация и температура электронов выше области ускорения. Экспериментально в большом числе работ, начиная с работ Lyons et al. [1979], Bosqued et al. [1986], была продемонстрирована линейная связь потока высыпающихся электронов от продольного падения потенциала с коэффициентом пропорциональности, не зависящим от широты, что означало примерное постоянство
- концентрация и температура электронов выше области ускорения. Экспериментально в большом числе работ, начиная с работ Lyons et al. [1979], Bosqued et al. [1986], была продемонстрирована линейная связь потока высыпающихся электронов от продольного падения потенциала с коэффициентом пропорциональности, не зависящим от широты, что означало примерное постоянство ![]() и
и ![]() . При исследовании мультиплетных структур типа перевернутого Vна базе данных спутника Интеркосмос-Болгария-1300 (см. Антонова и др. [1991], Antonova et al. [1998] было продемонстрировано отсутствие зависимости ионной температуры от широты в авроральном овале. Отсутствие такой зависимости для электронов было продемонстрировано в работах Антонова и др.[1998]. На рис. 1 (см. Антонова и др. [1998]) показано распределение электронной и ионной температур
. При исследовании мультиплетных структур типа перевернутого Vна базе данных спутника Интеркосмос-Болгария-1300 (см. Антонова и др. [1991], Antonova et al. [1998] было продемонстрировано отсутствие зависимости ионной температуры от широты в авроральном овале. Отсутствие такой зависимости для электронов было продемонстрировано в работах Антонова и др.[1998]. На рис. 1 (см. Антонова и др. [1998]) показано распределение электронной и ионной температур 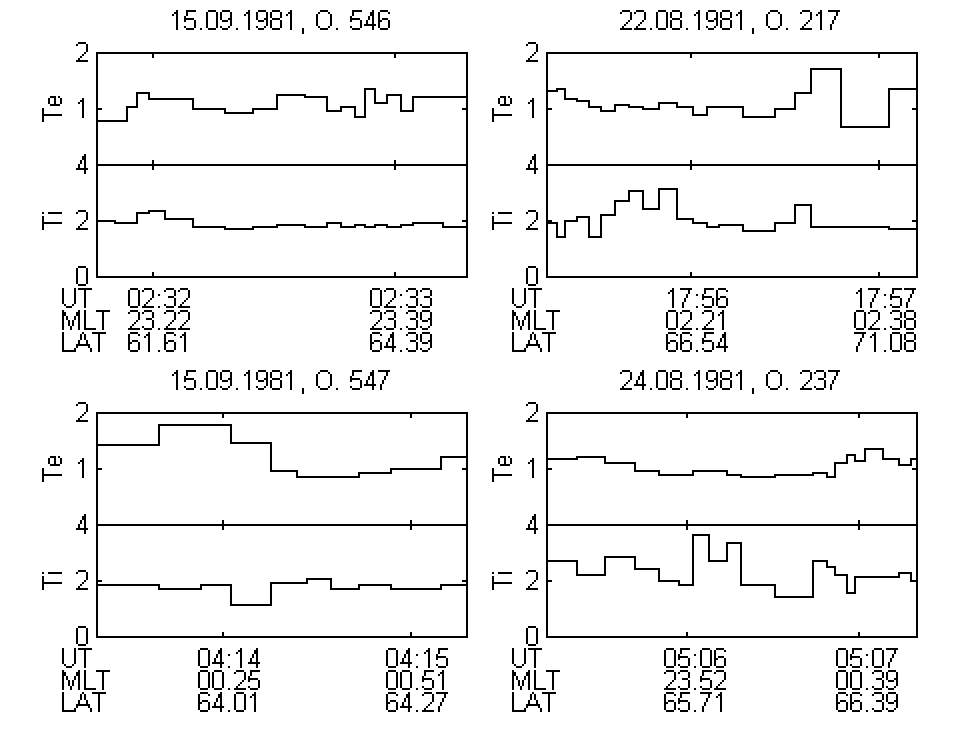
![]() много больше характерного времени электрон-ионных столкновений
много больше характерного времени электрон-ионных столкновений ![]() . При этом считается, что взаимодействие волна-частица либо столкновения с неоднородностями магнитного поля могут эффективно заменить кулоновские столкновения без изменения вида самих уравнений.
. При этом считается, что взаимодействие волна-частица либо столкновения с неоднородностями магнитного поля могут эффективно заменить кулоновские столкновения без изменения вида самих уравнений.![]() описания плазмы при отсутствии источников и стоков частиц включает (см. напр. Брагинский [1963]) уравнение непрерывности (закон сохранения числа частиц):
описания плазмы при отсутствии источников и стоков частиц включает (см. напр. Брагинский [1963]) уравнение непрерывности (закон сохранения числа частиц):
![]()
 (7)
(7) 
![]()
 (8)
(8)
<где p – полное давление, j – плотность электрического тока, B –магнитное поле, а в силу F (в большинстве случаев малую по сравнению с другими членами) входят вязкость, электрические силы и могут входить силы неэлектрической природы; уравнение баланса тепла (закон сохранения энергии):
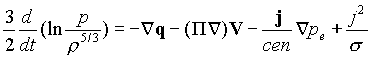
 (9)
(9)![]() -тензор вязкости,
-тензор вязкости, ![]() - проводимость.
- проводимость. 
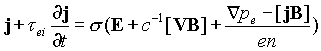
 (10)
(10)![]() - давления электронов. Если скорость движения плазмы много меньше звуковой ~
- давления электронов. Если скорость движения плазмы много меньше звуковой ~
![]() и альвеновской
и альвеновской ![]() , а сила F мала, выполняется условие магнитостатического равновесия:
, а сила F мала, выполняется условие магнитостатического равновесия:
![]()
 (11)
(11)![]() , уравнение (11) приобретает вид
, уравнение (11) приобретает вид
![]()
 (12)
(12)![]() - давления ионов. Если градиенты электронного и ионного давлений параллельны, то из соотношения (11) следует, что
- давления ионов. Если градиенты электронного и ионного давлений параллельны, то из соотношения (11) следует, что ![]() и уравнение (12) распадается на два:
и уравнение (12) распадается на два: ![]() и
и ![]() , где
, где ![]() - параллельная и перпендикулярная компоненты электрического поля. Т.е., в данном случае, поперечная к магнитному полю компонента электрического поля не создает тока, а уравновешивает градиент ионного давления. Информация о градиентах давления, как правило, отсутствует, поэтому соотношение (13) часто необоснованно заменяется законом Ома в форме
- параллельная и перпендикулярная компоненты электрического поля. Т.е., в данном случае, поперечная к магнитному полю компонента электрического поля не создает тока, а уравновешивает градиент ионного давления. Информация о градиентах давления, как правило, отсутствует, поэтому соотношение (13) часто необоснованно заменяется законом Ома в форме
![]()
 (13)
(13)
В движущейся со скоростьюV системе координат ![]() ,где
,где ![]() . В случае бесстолкновительной плазмы применение (13) предполагает, что в результате развития каких-либо неустойчивостей в плазме генерируются волны или образуются неоднородности и рассеяние частиц на неоднородностях делает проводимость конечной. Однако, если неустойчивость развивается в плазме, дрейфующей со скоростью (1), то образующиеся неоднородности будут "вморожены" в движущуюся плазму (или средний импульс волн будет равен нулю), что делает неприменимым соотношение (13). Рис. 2 иллюстрирует данное утверждение.
. В случае бесстолкновительной плазмы применение (13) предполагает, что в результате развития каких-либо неустойчивостей в плазме генерируются волны или образуются неоднородности и рассеяние частиц на неоднородностях делает проводимость конечной. Однако, если неустойчивость развивается в плазме, дрейфующей со скоростью (1), то образующиеся неоднородности будут "вморожены" в движущуюся плазму (или средний импульс волн будет равен нулю), что делает неприменимым соотношение (13). Рис. 2 иллюстрирует данное утверждение.
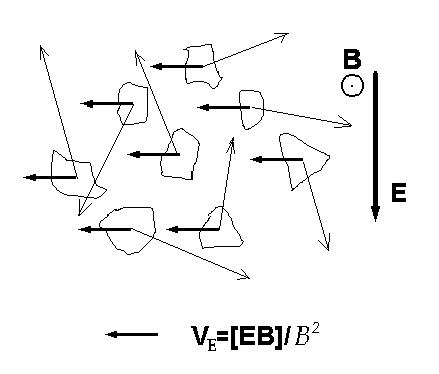 |
Рис. 2. Схема, иллюстрирующая возникновение неоднородностей "вмороженных" в движущуюся плазму. Толстыми стрелками показана скорость регулярного движения, тонкими - стохастического.
Таким образом, даже в случае плазмы с кулоновскими столкновениями закон Ома имеет достаточно сложный вид и требуется знание распределения давления для определения связи тока с электрическим полем. В случае бесстолкновительной плазмы даже наличие эффективных рассеивающих центров не дает возможности использовать простейшую форму закона Ома, предполагающую линейную связь поперечного тока с электрическим полем. Заметим также, что применение соотношения (13) делает необходимым учет омического нагрева ![]() , что, как правило, невозможно при аналитических рассмотрениях, а при численном моделировании требует достаточно больших машинных мощностей (МГД коды). При
, что, как правило, невозможно при аналитических рассмотрениях, а при численном моделировании требует достаточно больших машинных мощностей (МГД коды). При ![]() и
и ![]() (приближение холодной плазмы), из уравнения (12) следует уравнение вмороженности
(приближение холодной плазмы), из уравнения (12) следует уравнение вмороженности ![]() . Часто данное уравнение используется для определения локальных электрических полей по измерениям скорости и магнитного поля. Пренебрежение градиентами давления в таком случае может привести к большим ошибкам и неправильным выводам.
. Часто данное уравнение используется для определения локальных электрических полей по измерениям скорости и магнитного поля. Пренебрежение градиентами давления в таком случае может привести к большим ошибкам и неправильным выводам.
Невозможность измерения градиентов давления плазмы на первых этапах развития Космофизики привело к разработке многочисленных теоретических концепций, фактически постулировавших применимость столкновительной МГД для описания процессов в бесстолкновительной магнитосферной плазме. Часто предполагалось также, что для описания космофизических систем может быть использовано приближение вмороженности, которое нарушается только в локальных областях и на поверхностях разрыва, где происходит "магнитное пересоединение". Данный подход резко критикуется в монографии Альвена (Альвен [1983]), впервые получившего уравнение вмороженности, так как содержит ряд принципиально неразрешимых противоречий.
Совпадение связи тока с градиентом давления в бесстолкновительном и столкновительном случаях делает реальным предположение о возможности ее использования и для описания реальных космофизических объектов. Дивергенция поперечного тока в плазме определяет продольный ток, равный при выполнении соотношения (11) (см. Grad [1965], Vasyliunas [1970], Bostrom [1975], Тверской[1982]) на ионосферных высотах

![]()
 (14)
(14)
где n – вектор внешней нормали к ионосфере, W - объем магнитной силовой трубки с единичным потоком на уровне ионосферы

![]()
 (15)
(15)
где dl – элемент длины магнитной силовой линии и интегрирование проводится между сопряженными ионосферами.
В бесстолкновительной плазме легко возбуждаются различные неустойчивости, источниками которых могут быть градиенты давления, сдвиги скоростей, токи, пучки и.т.д. В большинстве случаев неустойчивости, генерирующие возмущения больших и средних масштабов, являются апериодическими, и развивается сильная турбулентность. До настоящего времени не разработана теория сильной турбулентности, позволяющая описывать пространственно-временные изменения параметров плазмы. В случае больших флуктуаций наблюдаемых гидродинамических параметров, средний поток ![]() , и гидродинамическое описание, в первом приближении, может быть заменено на диффузионное (см., например, Климонтович [1990]), при котором
, и гидродинамическое описание, в первом приближении, может быть заменено на диффузионное (см., например, Климонтович [1990]), при котором ![]() , где D – коэффициент турбулентной диффузии.
, где D – коэффициент турбулентной диффузии.


|