
НИИЯФ

 |
 |
НИИЯФ  |
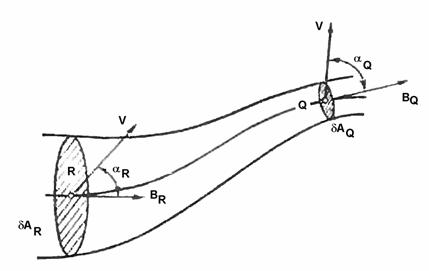
Пусть захваченные частицы движутся так, что их ведущая
силовая линия проходит через точки R и Q
в пространстве (Рис. 1). В дальнейшем
все величины, относящиеся к точкам
R и Q, будем
обозначать соответствующими индексами. Построим малые площадки
dAR,
dAQ
которые перпендикулярны силовой
линии. Пусть скорости частиц V, а питч углы находятся в интервалах
aR + daR и aQ + daQ.
Пусть магнитное поле равно
BR, BQ, импульсы частиц pR, pQ
Как говорит теорема Лиувилля для захваченных частиц,
направленные потоки
jR, jQ.
![]()
Если магнитное поле не меняется во времени и силовые линии
эквипотенциальны или внешние силы отсутствуют, то
p=const, jR (cos aR) = jQ(cos aQ) = const
Положим, как это часто бывает удобно в радиационных поясах
Земли, что питч-угловое распределение имеет вид колокольчика с максимумом
вблизи 90 градусов. Такие распределения с некоторой (к несчастью, не очень
большой) точностью аппроксимируют функциями типа
jR = jR0 (sin N aR)
Число N обычно называют показателем
анизотропии питч-углового распределения. Выясним, какой вид будет иметь
питч-угловое распределение в точке Q
в таком случае.
Из сохранения первого адиабатического инварианта следует, что
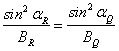 , откуда выражаем
, откуда выражаем
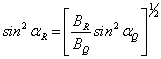
Тогда
![]()
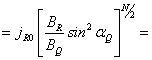
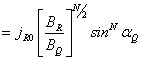
Видим, что питч-угловое распределение в точке
Q
будет иметь приблизительно тот же
вид (тот же показатель анизотропии), что и в точке
R, за исключением коэффициента перед
знаком синуса. Вводя обозначение вида
jQ = jQ0 (sin N aQ)
получим, что
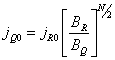
Таким образом, формы питч-углового распределения в разных
точках силовой линии будут подобны, а именно синус в некоторой степени.
Меняться будет лишь коэффициент перед синусом. Значение этого коэффициента
будет зависеть от отношения напряженностей магнитного поля в степени
N/2, где N– показатель анизотропии
питч-углового распределения.
Рассмотрим частный пример. Пусть
R
– экваториальная точка силовой линии,
Q – вне экватора.
Обозначим для
упрощения записи BR = B0, BQ = B,
jR0 = j0, jQ0 = j
Тогда, подставляя, получим
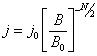
Примеры питч-угловых распределений для
N=4 и B/B0 = 1, 1.2, 1.5 показаны на
рис. 2.
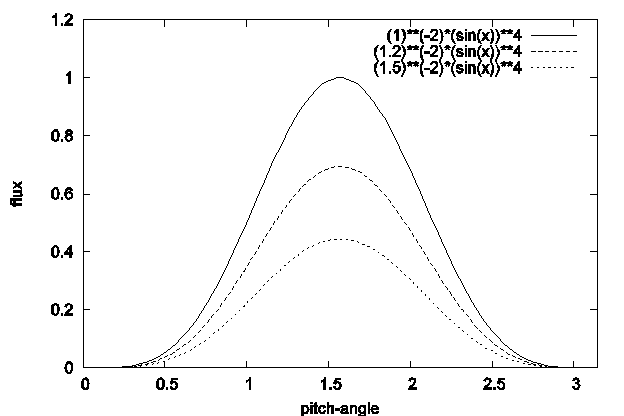 Рис. 2.
Рис. 2.
Приношу огромную благодарность Свиридову А.В. за помощь в выводе этих соотношений.
Литература:
Х. Редерер, Динамика радиации, захваченной геомагнитным
полем. Мир, Москва, 1972.