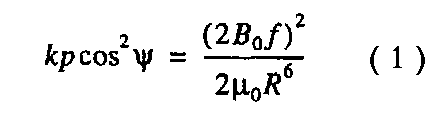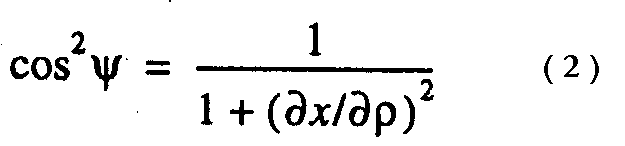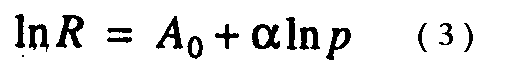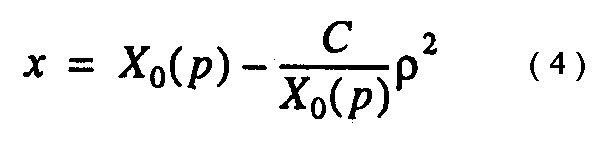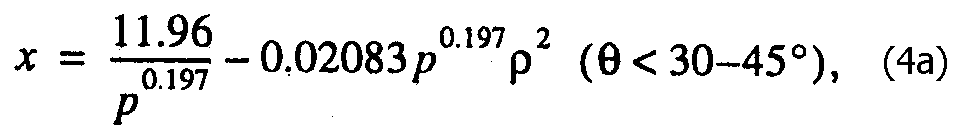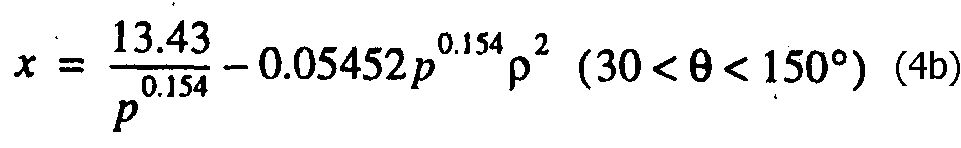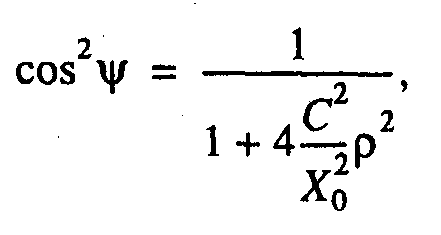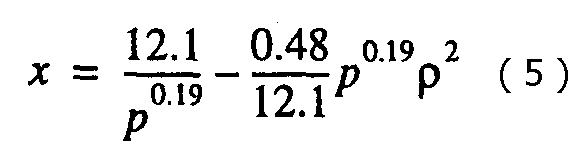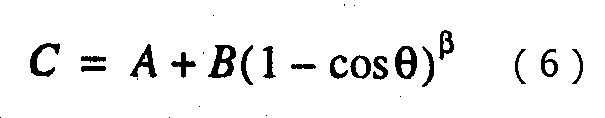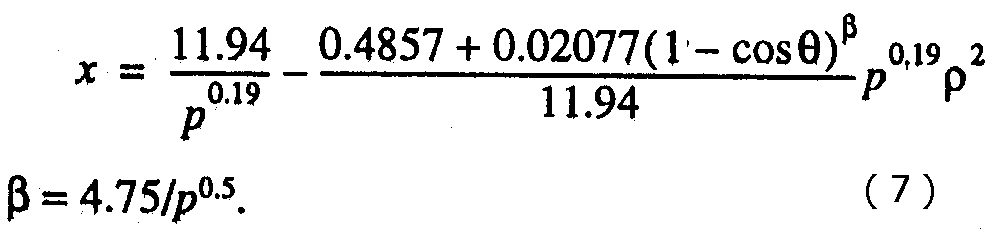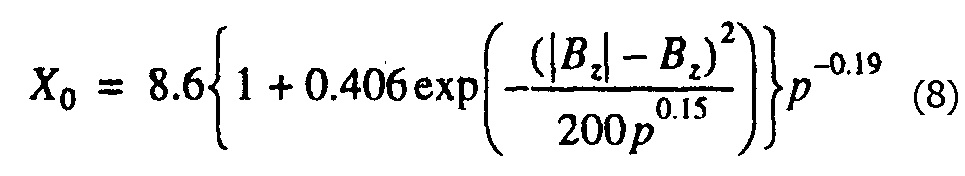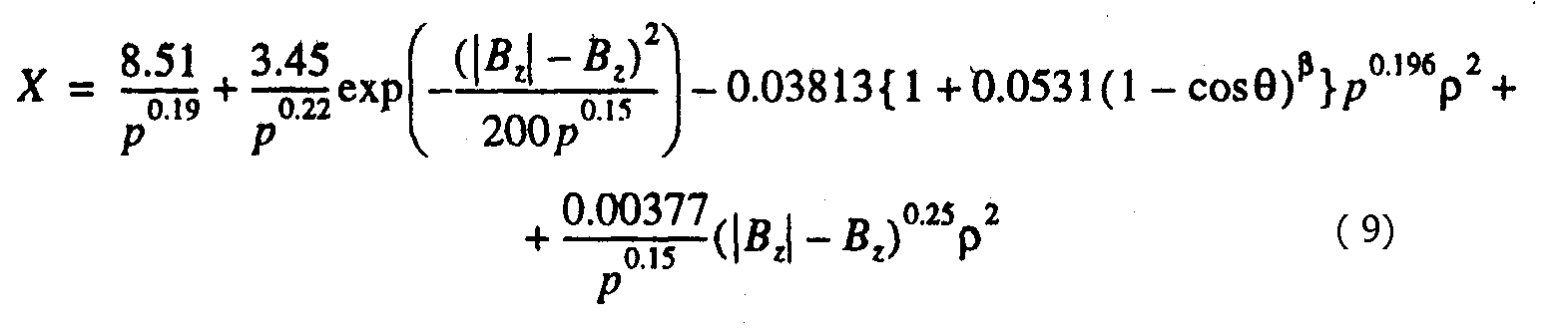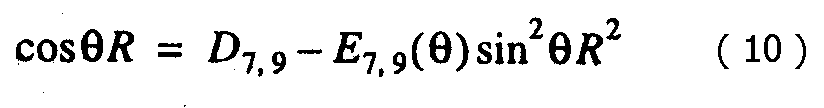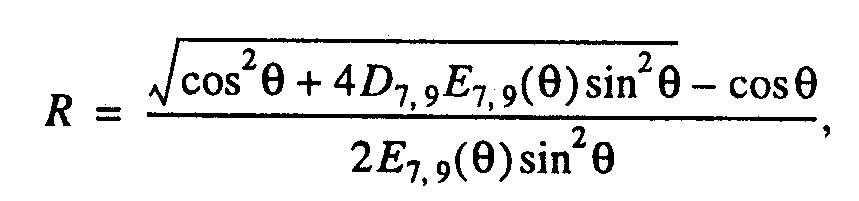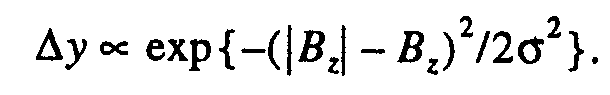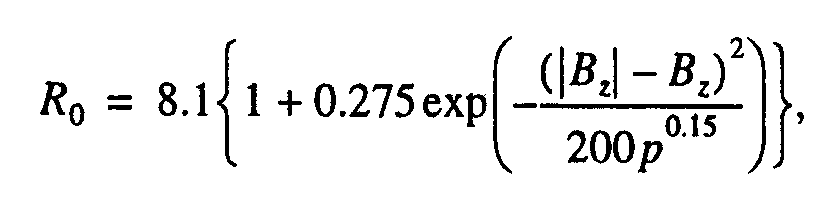
Солнечно-земная Физика

С. Н. Кузнецов, А. В. Суворова, А. В. Дмитриев

ФОРМА И РАЗМЕРЫ МАГНИТОПАУЗЫ.
СВЯЗЬ С ПАРАМЕТРАМИ МЕЖПЛАНЕТНОЙ СРЕДЫ

ГЕОМАГНЕТИЗМ И АЭРОНОМИЯ Том 38 1998 № 6. стр. 7-16

На большом массиве данных о пересечениях магнитопаузы различными спутниками на расстоянии от 5.2 Rз до 30-40 Rз построена модель магнитопаузы, начиная от лобовой точки вплоть до угла θ от направления на Солнце до 130-150°. Опреде-лены зависимости формы магнитопаузы и расстояния до произвольной ее точки от параметров межпланетной среды. В качестве параметров, контролирующих разме-ры и форму магнитопаузы, использованы среднечасовые данные о динамическом давлении солнечного ветра и Вz компоненты межпланетного магнитного поля. Получено, что при одном и том же давлении при Вz < -10 нТл магнитопауза оказыва-ется на ~30% ближе к Земле, чем при Вz > 0.

Введение

Определение формы и размеров магнитосферы и параметрическое описание ее геометрических характеристик как функций изменяющихся свойств плазмы солнечного ветра и межпланетного магнитного поля (ММП) является важной задачей магнитосферной физики. Очевидно, что решение этой задачи дает возможность создавать более обоснованные модели магнитосферы, чем существующие ныне и позволяет более детально изучать такие магнитосферные процессы как бури и суббури и распределение плазмы в магнитосфере. Этой теме посвящено несколько работ как экспериментальных [1-5], так и теоретических [6-10]. Теоретические работы показали, что в первом приближении магнитопауза имеет форму параболоида вращения или части эллипсоида вращения [8-10], были определены эмпирические зависимости размеров и формы магнитопаузы от параметров солнечного ветра и межпланетного магнитного поля: р - динамического давления плазмы и Вz ММП. В некоторых рабо-тах [11-14] исследовалось положение магнитопаузы при экстремальных значениях параметров солнечного ветра р > 20 нПа при Вz > 0 и Вz < - 6 нТл При р < 3 нПа. Для такого изучения использовались спутники на геостационарной орбите.

Экспериментальные данные

Для исследования связи размеров и формы магнитопаузы (МП) с параметрами солнечного ветра мы использовали массив данных о пересечениях границы магнитосферы высокоапогейными спутниками, предоставленных в наше распоряжение д-ром Д. Сайбеком (Университет Дж. Хопкинса). К этому массиву мы добавили данные о пе-ресечениях магнитопаузы геостационарными спутниками [11-14] и из сети Интернет. Данные о межпланетной среде брались из OMNI Web в сети Интернет.
Эмпирическая модель МП основана на 842 пересечениях МП, для которых были известны параметры солнечного ветра.

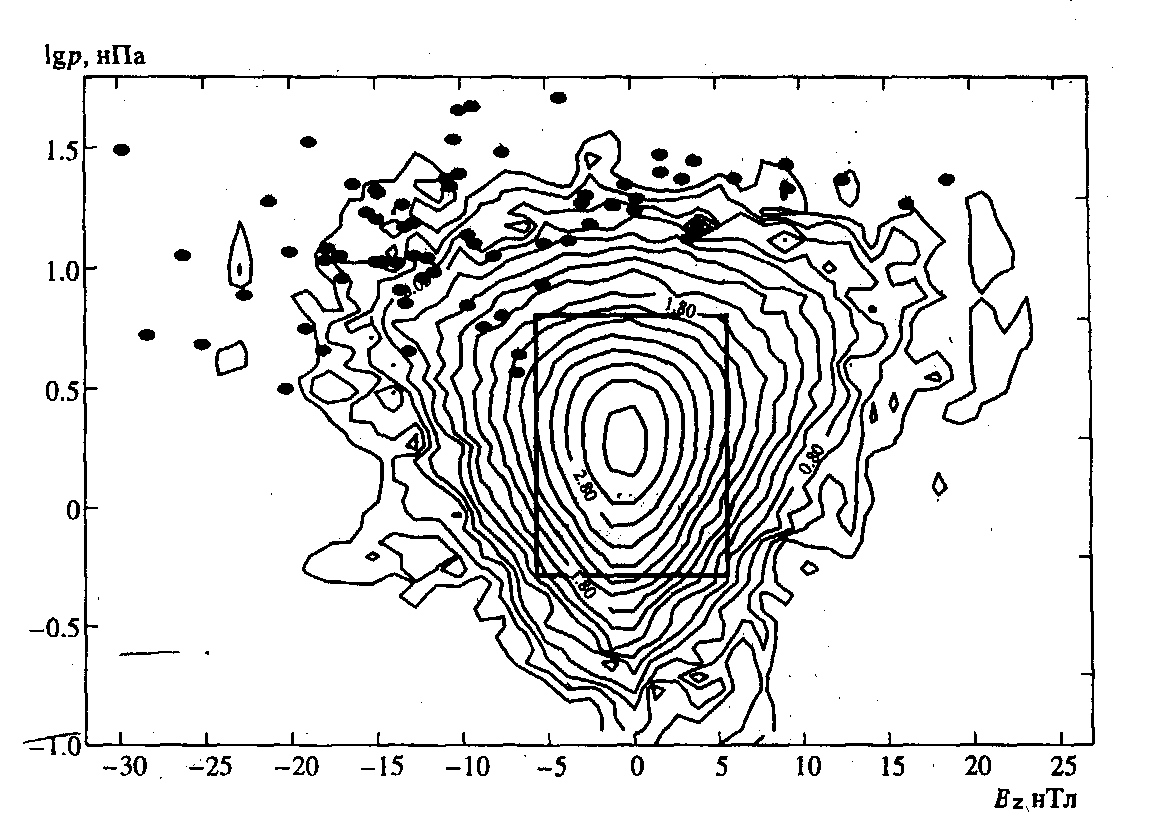
Рис. 1. Параметры солнечного ветра за ЗО-летний период наблюдений (более 100000 среднечасовых значений): логарифм динамического давления и Bz ММП. Показаны области наблюдения МП, наложенные на распределение Вz и lgp: прямоугольник - область соответствующая данным из массива д-ра Д. Сайбека, темные кружки - наблюдения МП на геостационарных спутниках.

На рис. 1 представлено распределение вероятности (в относительных единицах) регистрации определенных значений {lg p, Вz} за весь 30-летний период наблюдений параметров межпланетной среды до 1996 года. Видно, что наиболее вероятное значение р = 2 нПа и Bz ~ 0 нТл. Массив данных о пересечений МП различными высокоапогейными спутниками позволяет достаточно надежно определить зависимость по-ложения МП от р и Bz внутри прямоугольника, показанного на рисунке -6 < Вz < 6 нТл;0.5 <р < 8 нПа. На рисунке (точками)также отмечены случаи регистрации МП на геостационарных спутниках (R=6.6Rз). Включение данных геостационарных спутников позволяет расширить область моделирования МП при Bz > 0 до давлений ~25-30 нПа. В условиях, когда Вz < О, МП наблюдается на R = 6,6 даже при достаточно низком давлении ~3-4 нПа, что указывает на сильную зависимость положения МП от отрицательного Bz. Таким образом, включение данных геостационарных спутников позво-ляет существенно уточнить зависимость положения МП от Вz.

Анализ данных

При анализе данных мы предполагали справедливость уравнения баланса давлений на магнитопаузе [15].

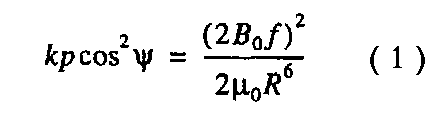где р - динамическое давление невозмущенного СВ; ψ - угол между внешней нормалью к МП и линией Земля-Солнце; μ_o - магнитная проницаемость вакуума; Вo - величина магнитного поля на поверхности Земли в экваториальной плоскости (3.1 х 104 нТл); R - расстояние от центра геомагнитного диполя до данной точки МП в радиусах Земли Rз; k - числовой параметр, характеризующий эффективность взаимодействия СВ с МП; f - учитывает отличие между геомагнитным полем на МП и удвоенным дипольным на данном расстоянии.
Заметим, что в ряде задач, в частности, при анализе уравнения баланса (1), требуется определить нормаль к магнитопаузе. В первом приближении аксиальной симметрии относительно оси X, направленной на Солнце, форму МП можно представить в виде
Р = f(x), р²=y²+г²,
и, используя следующие соотношения:
tg φ= dp/dx, а φ = 90° - ψ , и, следовательно, cosφ = sinψ,
можно получить формулу для вычисления нормали к МП

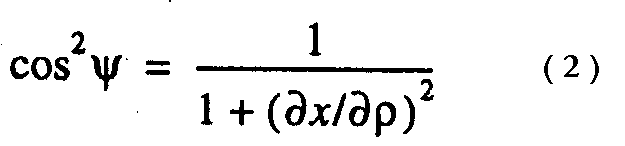На первом этапе мы исследовали связь между R и р для различных углов θ в диа-пазоне от 0 до 150° между векторами, направленными из центра диполя на Солнце и на данную точку МП. Коэффициент корреляции вычислялся для данных в интервале θ_o ± 5°, и каждый последующий интервал сдвигался на 5°. Число точек в интервалах колебалось от 10 до 40. Кроме того, по величине Bz было выделено три группы подмассивов: Bz > 0, - 3 < Bz < 0, Bz < - 3 нТл.
Исходя из теоретической зависимости между R и р (1), анализ экспериментальных данных проводился с помощью линейного регрессионного уравнения вида:

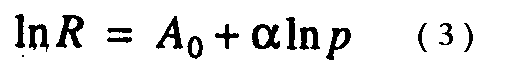На рис. 2 представлены результаты корреляционно-регрессионного анализа:
связь между модулем коэффициента а и коэффициентом корреляции r(lnR, Lnp) для 3-х Вz-подмассивов. Видно, что там, где наблюдается слабая корреляция между R u p, значения α малы, т.е. меньше теоретического значения α= 0.1666. С улучшением корреляции (r > 0.5) соответственно возрастает коэффициент линейной регрессии (|α|>0.16). Видно также, что хорошая корреляция связана с наиболее вероятным значением |α| ~ 0.19. Отметим, что из этого анализа (предварительные результаты опубликованы в [16]) следует, что подавляющее большинство θ-подмассивов, давших небольшие значения α| < 0.1 и низкий коэффициент корреляции |г| < 0.5, находилось в интервале углов θ > 70°, соответствующих флангам и хвосту магнитопаузы.

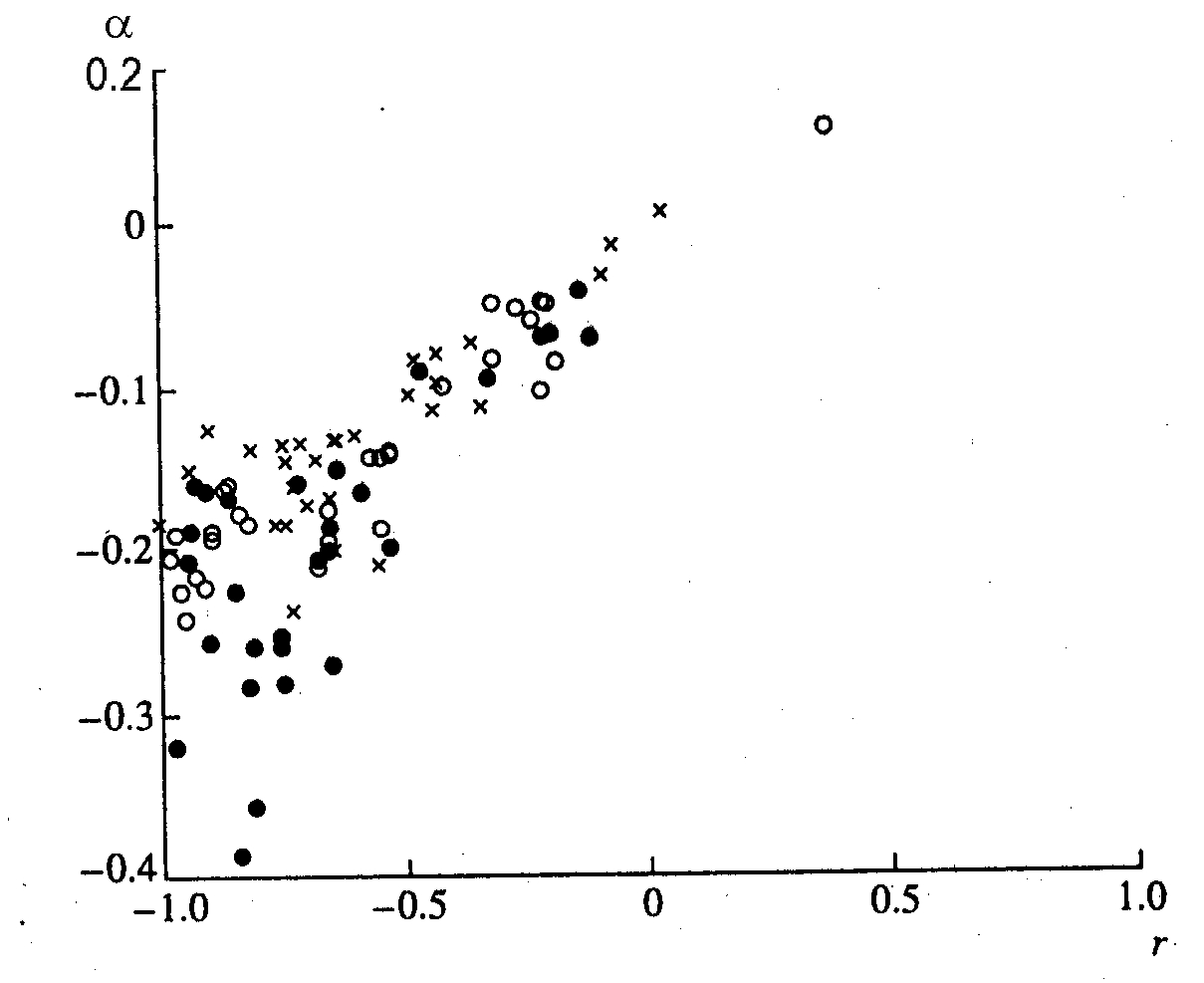
Рис. 2. Зависимость коэффициента ? из уравнения (3) от коэффициента корреляции r между lпR и lnp. Светлые кружки - для Вz > 0 нТл, кресты - для 0 > Bz > - 3 нТл, темные кружки - для Bz < - 3 нТл.

На следующем этапе мы исследовали форму магнитопаузы для Bz > 0 нТл. Мы используем параболоидную модель магнитопаузы и предполагаем, что при изменении давления форма МП сохраняется, меняется только ее размер, т.е. МП остается по-добной самой себе. В данном случае мы можем записать уравнение МП в виде:

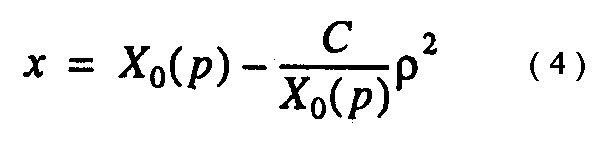
где С = const.
Анализ показывает, что для Вz > 0 наиболее оптимальным образом МП аппроксимируется двумя отрезками параболы:

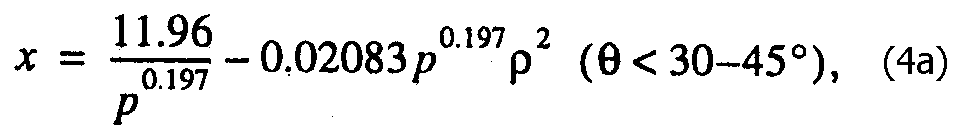
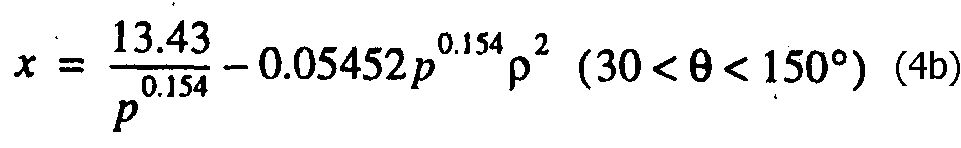
В уравнении (4а) С = 0.2492, в уравнении (4b) С = 0.7322.
Для рассматриваемого частного случая параболической аппроксимации (3) нормаль к магнитопаузе (2) вычисляется из следующего выражения:

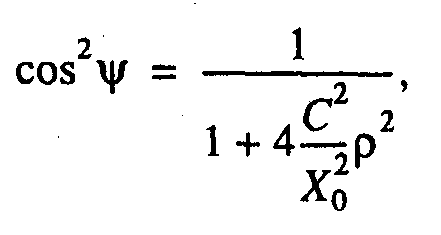где вместо Хо и С нужно подставить коэффициенты из (4а) или (4б) (для каждой из двух ветвей параболы, соответственно).
Следует отметить, что при изменений θ в пределах, от 0 до 50^о для носовой параболы численный коэффициент при Хо менялся от 11.86 до 12.1, а α изменялось в пределах 0.19-0.2.
Подобный результат (аппроксимация МП несколькими параболами) был получен нами ранее [4] по существенно меньшему материалу.
В работе [17] предлагалась упрощенная модель МП (одна парабола) для θ < 100-110°.

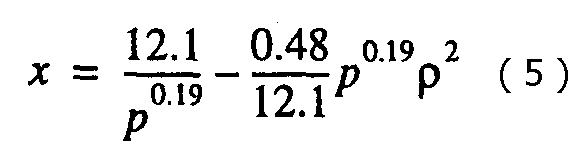Отмечалось также, что в интервале углов θ ~ 30-45° модель дает систематически заниженные значения R приблизительно на 10%. Анализируя кривую, которая получается из (4а) и (4б), мы заметили, что величину С можно представить как функцию θ, которая увеличивается с увеличением θ, в виде:

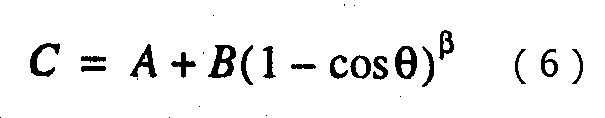
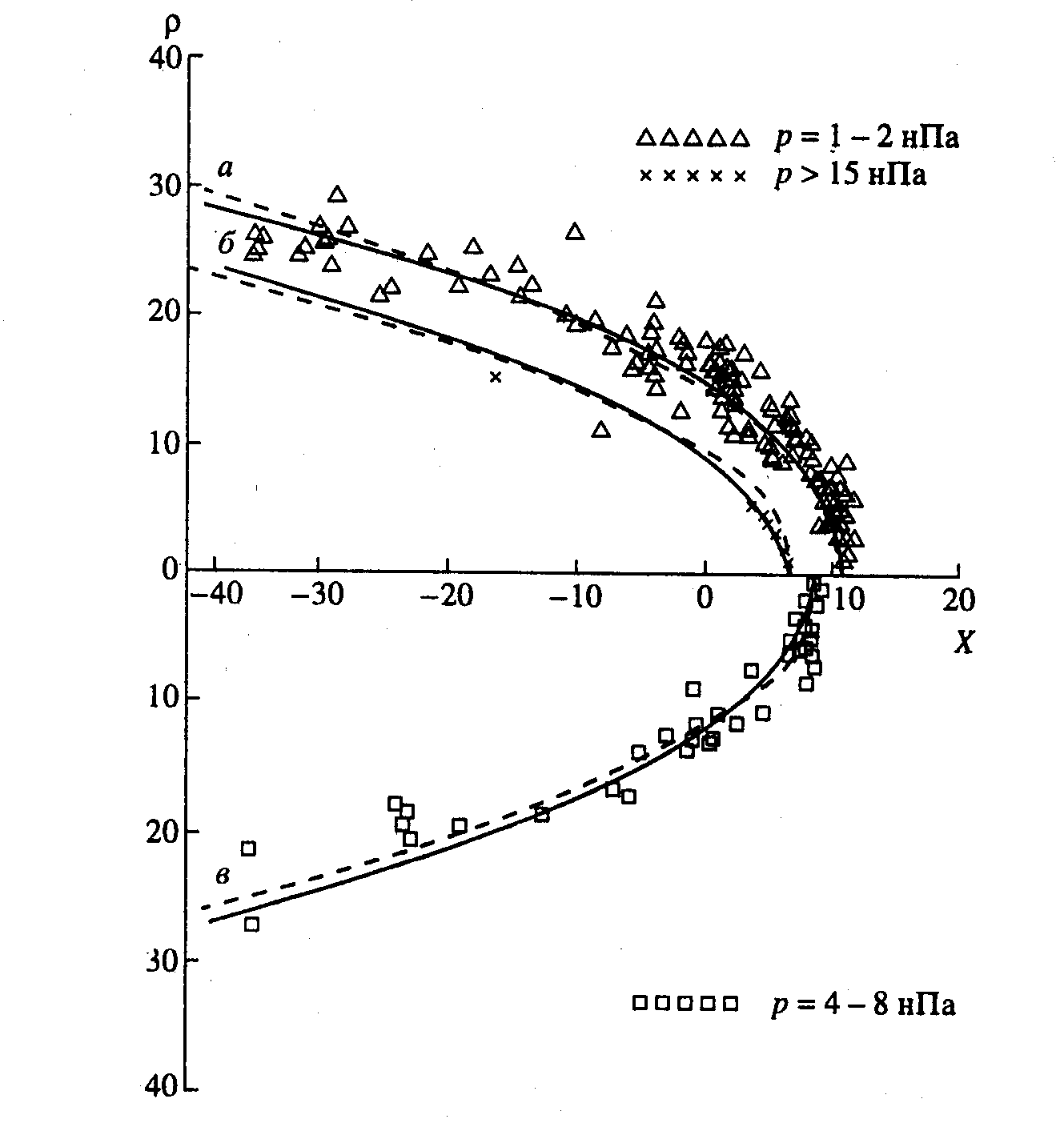
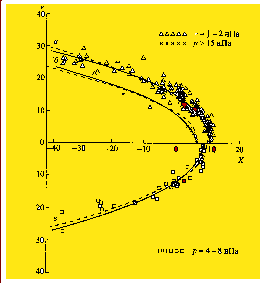
РИС. 3 Форма и размеры магнитопаузы при Вz > 0 нТл для: а - р = 1.7 нПа, б - р = 24 нПа, в - р = 6 нПа. Штриховая линия - вычисления с использованием уравнений (4а) и (4б), сплошная линия - с использованием уравнения (7). Экспериментальные данные: треугольники - для 1 < р< 1 нПа, квадраты - для 4 <р < 8 нПа, кресты - для р > 15 нПа.

Многомерный регрессионный анализ дал следующую функцию для описания МП для интервала θот 0 до 150°.

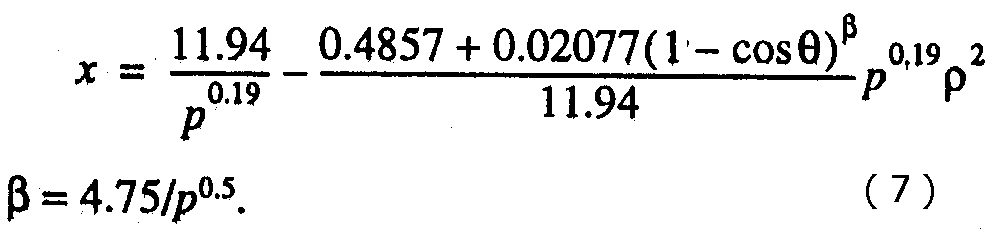Для θ< 90° выражения (5) и (7) близки, существенное различие возникает при θ> 90°. Таким образом, модель, состоящая из двух парабол, более точно описывает МП при θ = ЗО-4О0. На рис. 3 представлены экспериментальные точки для интервалов давлений р = 1-2; 4-8; >15 нПа и Bz > 0 и аппроксимация МП по формулам (4а), (4б) и (7).
В работе [12] указывалось, что в значительной части пересечений МП на геостационарной орбите наблюдалась эрозия магнитного поля. Анализ зависимости минимальных значений р от Вz для пересечений МП на R = 6.6Rз показал, что при Вz > О отношение коэффициентов f²/k в уравнении баланса давлений (1) приблизительно равно. 1-1.4. При уменьшении Вz до -6 нТл величина f²/k также уменьшается до ~0.25 и при дальнейшем уменьшении Вz сохраняет это значение. В [17] было предложено для аппроксимации положения носовой точки МП при любых Вz использовать выражение:

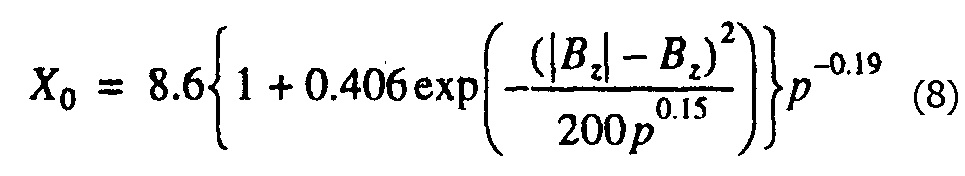
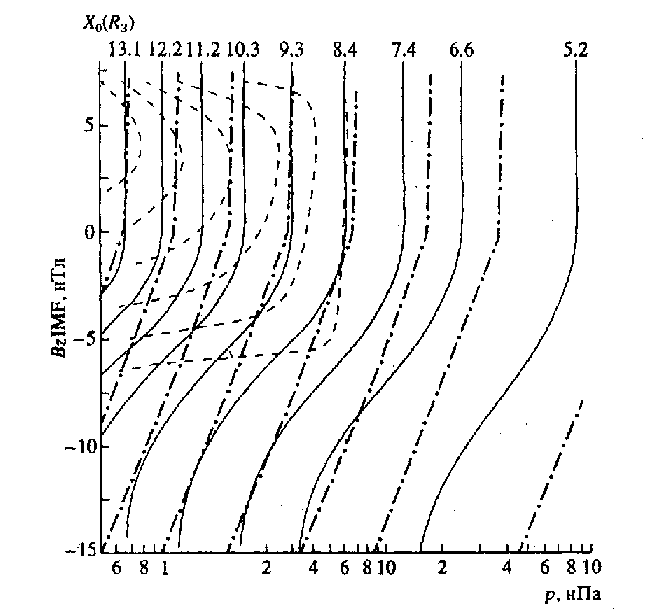
Рис. 4. Зависимость положения носовой точки магнитопаузы Xo от Bz u p для Xo = const. Значения Xо приве-дены сверху. Сплошные кривые - уравнение (8), штриховые - работа [2], штрихпунктирные - работа [5].

Анализ положения лобовой точки при аппроксимации МП показал, что в выражении (8) числовой множитель в знаменателе показателя экспоненты меняется от 120 до -ЗОО при увеличении верхнего предела θ в анализируемом массиве от 45 до 150°. Такое изменение числового множителя означает, что f²/k изменяется на интервале Bz от -5.5 до -8.5 нТл (множитель 200 соответствует Bz ~ -7 нТл). На рис. 4 пред-ставлены линии Хо = const в полулогарифмических координатах {lgp, Bz} по данным [2, 5] и настоящей работы. Видны различия в трех предлагаемых моделях.
При введении зависимости Хo от Bz необходимо ввести и зависимость С от Bz. Если мы сохраним зависимость С от θ (6), то Х станет функцией пяти аргументов. Вследствие этого значительно уменьшается точность найденного решения. Тем не менее, мы можем для всех Bz записать выражение для определения МП в виде:

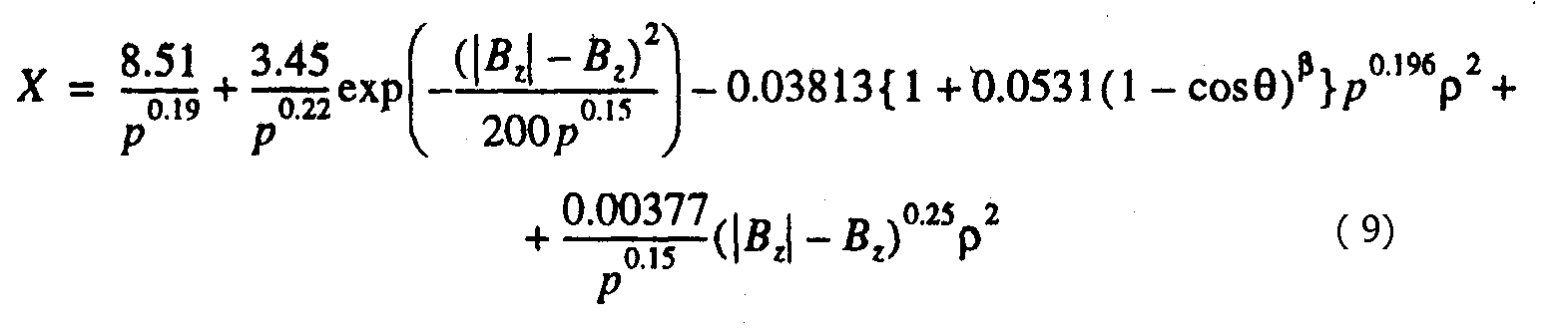где β- то же самое, что и в выражении (7). Последний член описывает зависимость С от Вz. В [17] использовалась линейная зависимость, но многомерный статистичес-кий анализ показал, что лучше использовать степенную функцию.

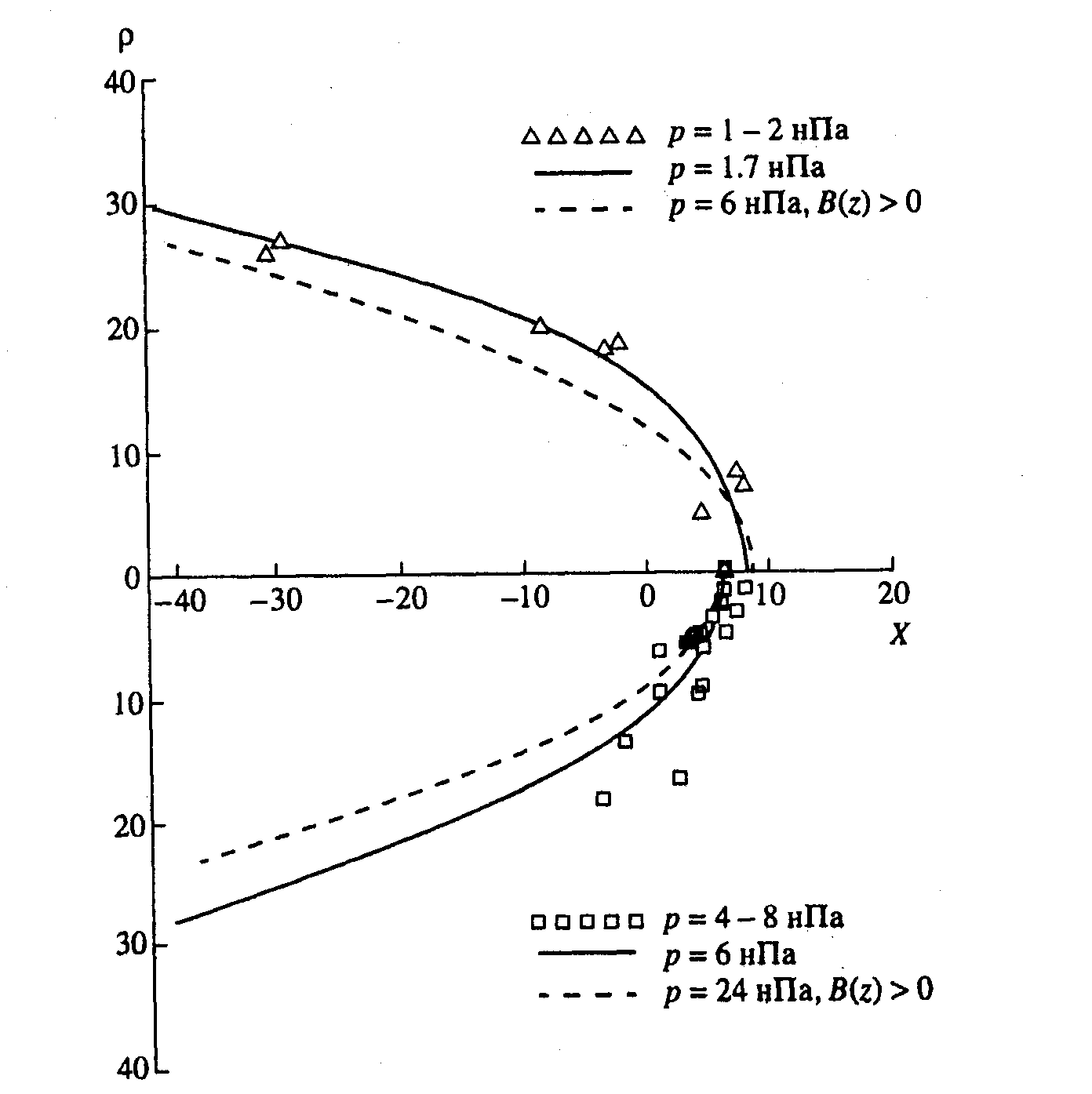
Рис 5. Форма и размеры магнитопаузы при Bz = - 10 нТл для p = 1.7 нПа (сверху) и 6 нПа (внизу) (вычисления по формуле (9) - сплошная линия) и при Bz > 0 для р =6 иПа (вверху) и 24 нПа (внизу) (вычисления с использованием уравнения (7) - штриховая линия). Экспериментальные данные отобраны для Bz < - 6 нТл; треугольники - для 1 < р < 2 нПа, квадраты: 4 < р < 8 нПа.,

На рис. 5 представлены экспериментальные точки для Вz < -6 нТл и давления р = 1- 2 нПа и р = 4-8 |нПа. Также приведены кривые, аппроксимирующие МП, рассчитанные по формуле (9). Видно хорошее согласие данных и модели.
Для сравнения формы и угла затупления магнитопаузы при Bz > 0 и Вz < 0 на рис. 5 пунктиром показаны аппроксимации для Bz > 0. В верхней части рисунка расчеты положения магнитопаузы с подсолнечной точкой около 8Rз, соответствуют давлению 1.7 нПа (Вz < - 6 нТл) и 6 нПа (Вz > 0). В нижней части рисунка модельные кривые с подсолнечной точкой около 6.5 Rз соответствуют давлению 6 нПа (Вz < -6 нТл) и 24 нПа (Вz>0). Видно, что угол затупления магнитопаузы при южном В, больше, чем при северном Bz Естественно, что наилучшее количественное согласие (в пределах статистических ошибок) данной модели с [2, 5] наблюдается в области наибольшей статистической обеспеченности данных (X > -20 Rз).
Следует отметить, что, используя непосредственно уравнения (7) и (9), нельзя в координатах [х, р] построить кривую, описывающую магнитопаузу. Необходимо уравнения (7) или (9) представить в виде:

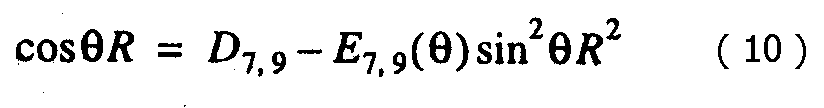и найти из уравнения (10) R для необходимого фиксированного θ:

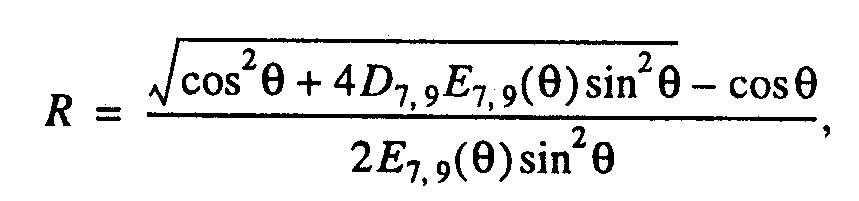а затем определить х = Rcos θ и ρ= sin θ
D7 - это член уравнения (7), описывающий положение носовой точки, D9 - соот-ветствующий член для уравнения (9). Е7, - коэффициент npu ρ² = R²sin²θиз уравнения (7), Е9 - соответствующий коэффициент из уравнения (9).
Различие давлений солнечного ветра при регистрации МП на утренней и вечерней стороне на R = 6.6 Rз заставило нас предположить [17,18], что носовая точка сдвинута на вечернюю сторону Земли. Для Вz > О этот сдвиг имеет величину Δy ~ 0.6-1 Rз, для Вz < -7 нТл этот сдвиг Δ ~ 1.5-2.2/Rз. Многомерный статистический анализ показы-вает, что при Хo > 6.6/Rз Для Вz > 0 этот сдвиг <1Rз и в пределах точности измерений им можно пренебречь, для Вz < 0 мы задавали сдвиг как функцию Вz.

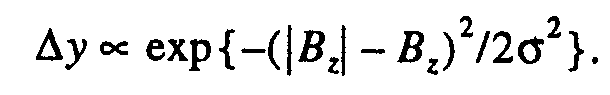В результате мы получили, что сдвиг не превосходил 2Rз, однако введение сдвига не изменяло коэффициента корреляции для нашей функции регрессии. Таким образом, для установления сдвига носовой части магнитопаузы при малых р (<4 нПа) тре-буются дальнейшие исследования.

Обсуждение результатов

В настоящее время имеются две работы [2,5], в которых проведен детальный анализ зависимости формы и размеров МП от р и Вz. Нами, как упрощенная модель МП, опубликована параболоидная модель МП [17] для θ < 110°. Следующие недостатки моделей необходимо отметить в первую очередь:
   а) магнитопауза не является поверхностью 2-го порядка. Положение носовой точ-ки мы можем определить, используя лишь данные при θ< 30-50°. Если использовать большое количество фланговых точек (θ > 40°), то, как правило, положение носовой точки будет завышено, этот вывод следует из [5] и из необходимости ввести вторую параболу для флангов по результатам наших исследований. Этот вывод остается в силе как для эллипсоидной [2], так и для параболоидной модели. В связи с этим в работе [5] был введен другой тип аппроксимирующей функции, а нами была введена зависи-мость коэффициента С в (4) от угла θ ;
   б) во всех предлагаемых моделях существенно отличается зависимость Хo от р. Анализ, проведенный в настоящей работе, а также в [16], показывает, что при различных θнаиболее вероятное значение α= 0.19 ± 0.02 характеризуется большим ко-эффициентом корреляции, хотя для флангов среднее значение α может снизиться до - 0.154 (см. формулу (4а) настоящей работы или [5]). По всей видимости, наиболее вероятное значение α> 1/6 связано с тем, что в уравнении баланса давлений на МП (1) коэффициент k является функцией давления;
   в) последний важный вопрос во всех моделях касается введения зависимости от Вz. В работе [2] в определенной мере зависимость от Вz была аналогичной зависимости от р, поэтому зависимость Хo от Вz при Вz > 0 и Вz < 0 были подобны (смотри рис. 4). В работе [5] принята линейная зависимость Хo (или Ro) от Bz разная для Вz > 0 и Вz < 0. Эта зависимость показана на рис. 8 указанной работы для р = 1.915 нПа. Отметим, что лучшей аппроксимацией этого графика является функция

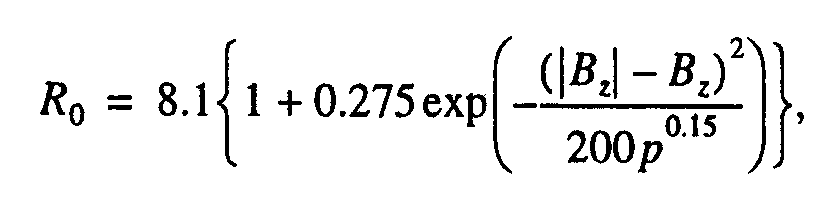то есть функция подобная выражению (8) в настоящей работе.

Заключение

Нами проанализирован большой массив данных о пересечениях магнитопаузы спутниками, накопленный до 1993 г. Нами предложена достаточно простая аппроксимация магнитопаузы при Вz> О для давлений 1-25 нПа или в виде двух парабол (4а), (46) или в виде единой функции (7) для θ < 150°.
Для всех Bz можно использовать выражение (9), которое включает зависимость Xo от Вz и С от Bz При Вz > 0 уравнение (9) вырождается и становится похожим на (7), различия между (7) и (9) непринципиальны.

Электронный вариант модели магнитопаузы и расчеты нормали к ней представлен на www-странице: http:/alpha.npi.msu.su/~alla.
Мы благодарим д-ра Д. Сайбека из Университета им. Д. Хопкинса (США), предоставившего нам основную часть анализируемых пересечений магнитопаузы. Данные о параметрах солнечного ветра и межпланетного магнитного поля получены из информационных систем NASA/NSSDC.
Данная работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований по проекту 96-05-65075.

СПИСОК ЛИТЕРАТУРЫ

1. Fairfield D.H. Average and unusual locations of the Earth's magnetopause and bow shock // J. Geophys. Res. 1971. V. 76. P. 6700. 2. RoelofE.C., Sibeck D.G. The magnetopause shape as a bivariate function of IMF Bz and solar wind dynamic pressure //J. Geophys. Res. 1993. V. 98. A12. P. 21421. 3. Sibeck D.G., Lopez R.E., Roelof E.C. Solar wind control of the magnetopause shape, location, and motion// J. Geophys. Res. 1991. V. 96. A4. P. 5489. 4. Кузнецов С.Н., Застенкер Г.Н., Суворова А.В. Динамика дневной магнитопаузы в связи с условиями в межпланетной среде // Космич. исслед. 1992. Т. 30. № 6. С. 826. 5. Shue J.-H., Chao J.K., Fu H.C. et al. A new functional form to study the solar wind control of the magnetopause size and shape // J. Geophys. Res. 1997. V. 102. A5. P. 9497. 6. Ferraro V.C.A. An approximate method of estimating the size and shape of the stationary hollow carved out in a neutral ionized stream of corpuscles impinging on the geomagnetic field // J. Geophys. Res. 1960. V. 65. P. 3951. 7. Mead G.D. Deformation of the geomagnetic field by solar wind // J. Geophys. Res. 1964. V. 69. Р. 1181. 8. Иванов К.Г. Наклонное набегание потоков на магнитосферу// Геомагнетизм и аэрономия. 1968. Т. 8. № 1.С. 24. 9. Alekseev 1.1., Shabansky V.P. A model of magnetic field in the geomagnetosphere // Planet, and Space Sci. 1972. V./20. P. 117. 10. Tsyganenko NA. A solution of the Chapman-Ferraro problem for an ellipsoidal magnetopause // Planet, and Space Sci. 1989. V. 37. P. 1037. 11. Russel C.T. On the occurrence of magnetopause crossings at 6.6Re // Geophys. Res. Lett. 1976. V. 3. № 10. Р.593. 12. Rufenach C.L., Martin Jr.R.F„ Sauer H.H. A study of geosynchronous magnetopause crossings // J. Geophys. Res. 1989. V. 94. All. P. 15125. 13. McComas D.J„ Elphic R.C., Moldwin M.B.. Thomson M.F. Plasma observations of magnetopause crossings at geosynchronous orbit // J. Geophys. Res. 1994. V. 99. P. 21249. 14. Hoffman KA., Cahill C.J.,Anderson R.R. et al. Explorer 45(S3A) observations of the magnetosphere and magnetopause during August 4-6 1972 magnetic storm period // J. Geophys. Res. 1975. V. 80. P.4287. 15. Spreiter J.R., Summer A.L., Alksne A.Y. Hydrodynamic flow around the magnetosphere // Planet. Space Sci. 1966. V. 14. P. 223. 16. Kuznetsov S.N., Suvorova A.V., Zastenker G.N., Sibeck D.G. Solar wind control of the geomagneto-pause position // In: Proc. 1992 STEP Symposium. Cospar Colloguium Series. 1994. V. 5. P. 293. 17. Kuznetsov S.N., Suvorova A.V. An empirical model of the magnetopause for broad ranges of solar wind pressure and Bz IMF // In: Polar cap boundary phenomena, eds. by J. Moen, A. Egeland, M. Lockwood. NATO ASI Series. Kluwer Academic Publishers. Dordrecht. 1998. P. 51. 18. Кузнецов С.Н., Суворова А.Ф. Форма магнитопаузы вблизи геостационарной орбиты // Ге-омагнетизм и аэрономия. 1997. Т. 37. № 3. С .1. Научно-исследовательский институт ядерной физики Московского государственного университета

Для связи: lazutin@srd.sinp.msu.ru